Today I am going to talk about the Q parameter on the bands of an EQ. We will be going a little deeper than we normally do, but that’s the nature of the Q factor.
The Q setting is going to affect the bandwidth of an EQ band. This means how much or how little of the frequencies will be affected with a boost or a cut. [Q stands for Quality factor]
On a basic level, one can see that when changing the Q setting, the bandwidth either gets wider or more narrow. Why does it do this, what does that affect, and how do I know which setting to use? Keep reading.
1 kHz bell curve boost
This typical view (above) is often referred to as a ‘bell’ curve due to the upper portion’s resemblance to the shape of a bell. In regard to the bell curve above, it has a center frequency of 1 kHz and a boost of 12 dB. (The solid line represents a boost; the dashed line shows if it were a cut).
The Q parameter controls the shape of the EQ curve. High Q values use steeper curves, which affect a smaller range and allow you to pinpoint specific frequencies. Low Q values affect a wider range of frequencies and tend to sound more gentle when used subtly. Q is the ratio of center frequency to bandwidth, and if the center frequency is fixed, then bandwidth is inversely proportional to Q—meaning that as you raise the Q, you narrow the bandwidth, and when you lower the Q, you widen the bandwidth. Q is by far the most useful tool an EQ offers, allowing you to attenuate or boost a very narrow or wide range of frequencies within each EQ band. (More on bandwidth below)
When using EQs, we are concerned with how much of the bandwidth we are affecting. We do this in octaves. When dealing with frequencies (Hertz), a doubling of the number is raising one octave higher. Conversely, halving the number is lowering one octave. Middle C (on a piano) is roughly 262 Hz. Going up one octave higher, to the next C up on the piano, the frequency is twice that, or 524 Hz. Going to the C below middle C is 131 Hz.
In order to understand Q, we have to focus on two other details. The center frequency (the one we choose for the band, i.e. 1,000 Hz), also known as f0 , and the bandwidth (f2 – f1).
Looking at the graph below, we see a boost of 12 dB. But we measure the bandwidth 3 dB down from 12 dB, which is 9 dB. The width of this, measured in octaves, is what the Q sets. In our example above, if the center frequency is 1 kHz, we can set the Q to affect one octave, centered around 1 kHz. Or, 2 octaves, 1/2 octave, 1/3 octave, etc. [Remember, the bandwidth is always measured at 3 dB down from center frequency]
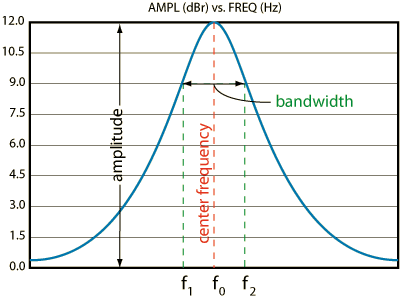
Q is defined as: Q = center frequency ÷ bandwidth
For example, a filter centered at 1000 Hz that is 1/3-octave wide has frequencies located at 891 Hz and 1123 Hz respectively, yielding a bandwidth of 232 Hz. Q, therefore, is 1000 Hz divided by 232 Hz, or 4.31. (Again, remember, this is 3 dB down from center frequency).
If you want to do a quick estimate of bandwidth, take the inverse of the Q number. A Q of 1 will refer to a one-octave bandwidth; a Q of 4 will be 1/4 octave; a Q of 2 will be 1/2 octave; a Q of 10 will be 1/10 of an octave. A Q of .25 would indicate a four-octave bandwidth. This will not give you a precise bandwidth, but will be close. The math behind these shortcuts is complicated. It’s a relatively complex multi-step algebraic formula that ties Q and the bandwidth together.
We can always refer to a table or chart for more precise numbers. The following table shows the frequencies of a Q setting for one-octave bandwidth (a Q setting of 1). Listed is the center frequency (which we set), along with the upper and lower frequency, for a one octave bandwidth.
Octave Bands
| Lower Band Limit (Hz) | Center Frequency | Upper Band Limit (Hz) |
| 11 | 16 | 22 |
| 22 | 31.5 | 44 |
| 44 | 63 | 88 |
| 88 | 125 | 177 |
| 177 | 250 | 355 |
| 355 | 500 | 710 |
| 710 | 1,000 | 1420 |
| 1420 | 2,000 | 2840 |
| 2840 | 4,000 | 5680 |
| 5680 | 8,000 | 11360 |
| 11360 | 16,000 | 22720 |
Conversion chart or table ‘bandwidth in octaves’ to quality factor Q
| BW in octaves | Filter Q | BW in octaves | Filter Q | BW in octaves | Filter Q | BW in octaves | Filter Q | |||
| 1/80 | 115.4 | 1 | 1.41 | 4 | 0.267 | 7 | 0.089 | |||
| 1/60 | 86.6 | 1 1/4 | 1.12 | 4 1/4 | 0.242 | 7 1/4 | 0.082 | |||
| 1/50 | 72.1 | 1 1/3 | 1.04 | 4 1/3 | 0.234 | 7 1/3 | 0.079 | |||
| 1/40 | 57.7 | 1 1/2 | 0.92 | 4 1/2 | 0.220 | 7 1/2 | 0.075 | |||
| 1/30 | 43.3 | 1 2/3 | 0.82 | 4 2/3 | 0.207 | 7 2/3 | 0.071 | |||
| 1/25 | 36.1 | 1 3/4 | 0.78 | 4 3/4 | 0.200 | 7 3/4 | 0.068 | |||
| 1/20 | 28.9 | 2 | 0.67 | 5 | 0.182 | 8 | 0.063 | |||
| 1/16 | 23.1 | 2 1/4 | 0.58 | 5 1/4 | 0.166 | 8 1/4 | 0.058 | |||
| 1/12 | 17.3 | 2 1/3 | 0.56 | 5 1/3 | 0.161 | 8 1/3 | 0.056 | |||
| 1/10 | 14.4 | 2 1/2 | 0.51 | 5 1/2 | 0.152 | 8 1/2 | 0.053 | |||
| 1/8 | 11.5 | 2 2/3 | 0.47 | 5 2/3 | 0.143 | 8 2/3 | 0.050 | |||
| 1/6 | 8.65 | 2 3/4 | 0.45 | 5 3/4 | 0.139 | 8 3/4 | 0.048 | |||
| 1/5 | 7.20 | 3 | 0.40 | 6 | 0.127 | 9 | 0.044 | |||
| 1/4 | 5.76 | 3 1/4 | 0.36 | 6 1/4 | 0.116 | 9 1/4 | 0.041 | |||
| 1/3 | 4.32 | 3 1/3 | 0.35 | 6 1/3 | 0.113 | 9 1/3 | 0.039 | |||
| 1/2 | 2.87 | 3 1/2 | 0.33 | 6 1/2 | 0.106 | 9 1/2 | 0.037 | |||
| 2/3 | 2.14 | 3 2/3 | 0.30 | 6 2/3 | 0.100 | 9 2/3 | 0.035 | |||
| 3/4 | 1.90 | 3 3/4 | 0.29 | 6 3/4 | 0.097 | 9 3/4 | 0.034 | |||
| 10 | 0.031 |
Here is yet another chart for select octave bandwidths.
Q factor as a function of the bandwidth in octaves
| Bandwidth in octaves | Filter Q factor |
| 3.0 wide | 0.404 low |
| 2.0 | 0.667 |
| 1.5 | 0.920 |
| 1.0 | 1.414 |
| 2/3 | 2.145 |
| 1/2 | 2.871 |
| 1/3 | 4.318 |
| 1/6 | 8.651 |
| 1/12 small | 17.310 high |
Below are some pictures using fabfilter’s Pro-Q with different Q settings. Sometimes pictures explain things easier. Hopefully this will show what I’ve tried to explain with words and calculations.




Alternative to Memorizing These Shortcuts:
Memorizing all of the numbers above is a bit of a task. Here is a way to calculate these Q’s simply. It’s certainly not perfect, but it does offer a way to find these Q’s quickly.
By multiplying the number 2.05 with the first Q setting, .667 (2 octave bandwidth), you get 1.37. When rounded up, this equates to 1.4 – a number very similar to the Q setting for 1 octave.
If you continue multiplying 2.05 by each number that comes after, you’ll be able to equate Q’s that are very closely related to the exact numbers above.
For example: 1.37 x 2.05 = 2.8 or roughly a 1/2 octave bandwidth
2.8 x 2.05 = 5.75 or roughly a 1/4 octave bandwidth
The numbers certainly aren’t exact, but they get you close enough to a workable number, all while having you memorize only 2 numbers – .667 and 2.05.
Personally, I don’t like this because to get to a 1/4 octave, you have to run the calculation 4 times. But if this works for you – go for it!
Conclusion:
Practically speaking, setting your Q and it’s bandwidth to an octave or an octave based setting, drastically increases the musicality of your mix. On wider settings it makes it sound more natural and musical, on narrow settings it allows you to know the notes that you are affecting.
Consider using these shortcuts and octave based equalization whenever you want a quick, and accurate way to affect your mix.
I hope you were able to hang in there for this whole discussion. If you got lost in any of this, continue to hit it again and again until you fully understand it. I had to. Go down the rabbit hole and chase this until you “get it!”
As always, I hope this helps!
And HEY! Make it a GREAT day!!
T

